2.4 Uniqueness of the solution
To narrow the possible number of solutions, we turn to the second order conditions. Positive definite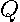 
would usually prove sufficient for an interior solution, but the vector 
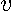embodies a polynomial constraint. Therefore, we elaborate on the second order conditions taking into account the constraints imposed by the structure of 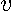. Consider the second derivative of the sum-of-squared errors with respect to 
shown in (
13
).
 | (13) |
The first term inside the brackets is positive because it represents a positive definite quadratic form. We can rewrite the second term in brackets as shown in (
14
),
 | (14) |
where 
equals,
 | (15) |
The minimum value of depends on the eigenvalues of 
. Note that 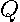is positive definite and the real diagonal (and thus Hermitian) matrix in (
15
) has two zero and 
positive eigenvalues. Horn and Johnson (1993, p. 465) state in Theorem 7.6.3 that the product of a positive definite matrix 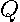and a Hermitian matrix has the same number of zero, positive, and negative eigenvalues as . Hence,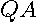 
must have two zero and positive eigenvalues. Therefore, is positive semidefinite implying that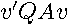 
has a minimum value of 0. Since the first term in brackets in (
13
) always has a positive value, the entire expression in (
13
) has a positive value and thus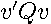 
is positive definite and strictly convex in . Hence, if an interior solution exists to the first order conditions, it must be unique.
There exists an interior solution to the first order conditions. To see this, examine the highest degree term in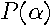 
, from (
11
) shown in (
16
).
 | (16) |
The term in brackets is the contribution to the overall sum-of-squared errors from the last term in the truncated Taylor’s series and must be positive. Since 
is even in , only the magnitude and not the sign of matter for this result. Since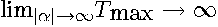 
, implies 
, there exists an interior solution to the first order conditions.
In conclusion, there exists a unique interior real , say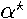 
, that minimizes the sum-of-squared errors and maximizes the MESS likelihood. Such unique optima are rare in spatial statistics. See Warnes and Ripley (1987) and Mardia and Watkins (1989)) for a discussion of the potential multimodality of the likelihood. The MESS unique closed-form optimum solution not only reduces computational time, but also increases the confidence users have in the numerical quality of the estimates.
