2.6 Spatial diagnostics
Christensen, Johnson, and Pearson (1992), Haining (1994), and Martin (1992) have investigated various aspects of diagnostics for spatial models. For the models which employ some form of estimated variance-covariance matrix  parameterized by a vector of parameters
parameterized by a vector of parameters 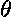 , estimating the model via maximum likelihood equates to estimating a model where both sides have been transformed (i.e.,
, estimating the model via maximum likelihood equates to estimating a model where both sides have been transformed (i.e.,  ). If the desire is to find leverage points with the transformed independent variables, this becomes difficult since the transformation depends upon
). If the desire is to find leverage points with the transformed independent variables, this becomes difficult since the transformation depends upon  . Fortunately, the right hand side of the MESS model in (
1
) does not involve parameters in the formulation of
. Fortunately, the right hand side of the MESS model in (
1
) does not involve parameters in the formulation of 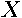 , so one can employ standard leverage statistics (avoiding one of the problems Martin (1992) examined). Since minimizing the overall sum-of-squared errors maximizes the likelihood, one can easily modify some of the useful diagnostics commonly employed in regression. Let
, so one can employ standard leverage statistics (avoiding one of the problems Martin (1992) examined). Since minimizing the overall sum-of-squared errors maximizes the likelihood, one can easily modify some of the useful diagnostics commonly employed in regression. Let 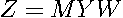 (hence
(hence 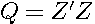 ), let
), let  , a
, a 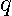 by 1 vector, and let
by 1 vector, and let 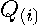 represent
represent 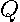 when deleting the
when deleting the  th observation. Applying the standard regression results for one-out sum-of-squared errors (e.g., Christensen (1996, p. 345)), produces (
22
).
th observation. Applying the standard regression results for one-out sum-of-squared errors (e.g., Christensen (1996, p. 345)), produces (
22
).

  | (22) |
Using the same quick mechanism for finding the roots of polynomials leads to a sequence of one-out autoregressive parameters  and one-out deviances. As well-known, each of these would correspond to the deviance associated with including a variable with 1 in the
and one-out deviances. As well-known, each of these would correspond to the deviance associated with including a variable with 1 in the  th row and zeros in all other rows (Christensen (1996, p. 348)).
th row and zeros in all other rows (Christensen (1996, p. 348)).
 Note, the case deletion diagnostics just consider the direct effect of a particular observation and do not account for their role in the transformation of the other observations. Naturally, one could delete blocks of observations and remove the observation itself, the observations it neighbors, and so forth (e.g. Christensen (1996, p. 348)).
Note, the case deletion diagnostics just consider the direct effect of a particular observation and do not account for their role in the transformation of the other observations. Naturally, one could delete blocks of observations and remove the observation itself, the observations it neighbors, and so forth (e.g. Christensen (1996, p. 348)).



