 3.3 Estimated parameters and deviances
3.3 Estimated parameters and deviances
Relative to a simple aspatial model of housing prices (i.e.,  ), the unrestricted log-likelihood rises from -266,505.2 to -228,850.4, a deviance of 75,309.6. Relative to a model with spatial independent variables, but no spatial transformation of the dependent variable (i.e.,
), the unrestricted log-likelihood rises from -266,505.2 to -228,850.4, a deviance of 75,309.6. Relative to a model with spatial independent variables, but no spatial transformation of the dependent variable (i.e.,  ), the deviance is 64,450.6. Controlling for some of the spatial dependence reduces the deviances associated with deletion of the independent variables and their spatial lags for three out of the four basic variables (i.e.,
), the deviance is 64,450.6. Controlling for some of the spatial dependence reduces the deviances associated with deletion of the independent variables and their spatial lags for three out of the four basic variables (i.e.,  ) relative to the corresponding deletions of the independent variables in the aspatial model (i.e.,
) relative to the corresponding deletions of the independent variables in the aspatial model (i.e., 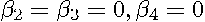 ). For the age variable, the deviance associated with deletion (i.e.,
). For the age variable, the deviance associated with deletion (i.e., 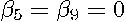 ) actually rises relative to the aspatial model (i.e.,
) actually rises relative to the aspatial model (i.e., 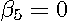 ).
).
 The interpretation and inferences based on estimated parameters from the aspatial and MESS models are quite different. For example, estimates from the aspatial model suggest that increasing income of a tract by 1% would lead to a 1.08% increase in median housing prices in the tract. Implicitly, the aspatial model allows for individuals with higher incomes to both purchase a larger house and to locate in a different neighborhood. For the MESS model where the characteristics of neighboring tracts is held constant, increasing the income of a tract by 1% would lead to only a 0.68% increase in median housing prices in the tract relative to median prices in surrounding tracts. This result is consistent with the economic construct of externalities (e.g., Bogart (1998, p. 216-218)).
The interpretation and inferences based on estimated parameters from the aspatial and MESS models are quite different. For example, estimates from the aspatial model suggest that increasing income of a tract by 1% would lead to a 1.08% increase in median housing prices in the tract. Implicitly, the aspatial model allows for individuals with higher incomes to both purchase a larger house and to locate in a different neighborhood. For the MESS model where the characteristics of neighboring tracts is held constant, increasing the income of a tract by 1% would lead to only a 0.68% increase in median housing prices in the tract relative to median prices in surrounding tracts. This result is consistent with the economic construct of externalities (e.g., Bogart (1998, p. 216-218)).
 The optimal number of neighbors was 30 (
The optimal number of neighbors was 30 (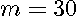 ) and the optimal rate of geometric decline with order was 0.9 (
) and the optimal rate of geometric decline with order was 0.9 ( ), and
), and  was -1.67. All of the deviances associated with perturbations in these choices were highly significant.
was -1.67. All of the deviances associated with perturbations in these choices were highly significant.
 It took slightly under 16 minutes on a 600 megahertz Pentium III computer running Matlab 5.3 to estimate the MESS model for each of the 203 cases defined by the grid over values of
It took slightly under 16 minutes on a 600 megahertz Pentium III computer running Matlab 5.3 to estimate the MESS model for each of the 203 cases defined by the grid over values of  and
and  0.25, 0.5, 0.75, 0.85, 0.90, 0.95, 1.0, implying that each regression took under 5 seconds. The Fortran 90 routines took only 132 seconds to perform the same computations. The speed gain from using Fortran 90 makes searches over these parameters rather easy. Figure 1 shows the profile log-likelihoods across these combinations of
0.25, 0.5, 0.75, 0.85, 0.90, 0.95, 1.0, implying that each regression took under 5 seconds. The Fortran 90 routines took only 132 seconds to perform the same computations. The speed gain from using Fortran 90 makes searches over these parameters rather easy. Figure 1 shows the profile log-likelihoods across these combinations of  and
and  (scaled by subtracting the maximum log-likelihood). Quick computation of the estimator allowed for the optimization of the transformation with respect to three parameters (
(scaled by subtracting the maximum log-likelihood). Quick computation of the estimator allowed for the optimization of the transformation with respect to three parameters ( ) despite the large size of the problem. Hopefully, such flexibility will approximate the true transformation.
) despite the large size of the problem. Hopefully, such flexibility will approximate the true transformation.


