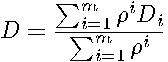3.2 Model
The overall transformed MESS model of housing prices appears in ( 23 ).

(23)

where 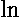denotes logarithm and 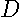is a row-stochastic spatial weight matrix.
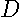Construction of first requires finding the nearest neighbors for each observation. One can use several algorithms for this, but all require at least 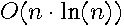operations for points on a plane (Eppstein, Paterson, and Yao (1997)). A Delaunay triangle based method was used here to compute the nearest neighbors.
A set of individual neighbor matrices 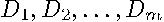, was formed where 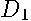represents the closest previously sold neighbor (shortest distance), 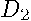represents the second previously sold neighbor (second shortest distance) and so on. These very sparse matrices have a 1 in each row and contain zeros elsewhere.
The overall spatial matrix 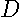was constructed based on the individual neighbor matrices 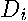using ( 24 ).
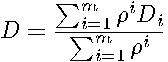(24)
In ( 24 ), 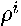weights the relative effect of the th individual neighbor matrix, so that depends on the parameters as well as in both its construction and the metric used. Thus ( 24 ) imposes an autoregressive distributed lag structure on the spatial variables. By construction, each row in 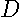sums to 1 and has zeros on the diagonal.
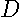The use of the individual neighbor matrices greatly speeds up investigation of the sensitivity of the results to different forms of . Constructing the individual neighbor matrices requires some computational expense, with the set of 30 used here taking 96.7 seconds computational time. However, reweighting the individual matrices using ( 24 ) requires very little time.